Linked List

Middle of a linked list

Approach: Fast and Slow Pointer

Time Complexity: O(N), where N is the number of nodes in the given list.

Space Complexity: O(1), the space used by slow and fast

class Solution { public: ListNode* middleNode(ListNode* head) { ListNode* slow = head; ListNode* fast = head; while (fast != NULL && fast->next != NULL) { slow = slow->next; fast = fast->next->next; } return slow; } };

Reverese a linked list

[Easy] No.206 Reverese Linked List

Approach: Iterative

Time Complexity: O(N), where N is the number of nodes in the given list.

Space Complexity: O(1)

class Solution { public: ListNode* reverseList(ListNode* head) { ListNode* prev = NULL; ListNode* curr = head; while(curr != NULL) { ListNode* nextTemp = curr->next; curr->next = prev; prev = curr; curr = nextTemp; } return prev; } };

[Medium] No.92 Reverse Linked List from index m to index n

Approach: Iterative

Time Complexity: O(N), We process each of the nodes at most once (we don't process the nodes after the nth node from the beginning).

Space Complexity: O(1) since we simply adjust some pointers in the original linked list and only use O(1) additional memory for achieving the final result.

Merge two sorted linked list

[Easy] No.21. Merge Two Sorted Lists

Approach: Iterative

Time Complexity: O(n+m), n is the length of l1 and m is the length of l2.

Space Complexity: O(1) The iterative approach only allocates a few pointers, so it has a constant overall memory footprint.

class Solution { public: ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) { ListNode* dummy = new ListNode(0); ListNode* iter = dummy; while(l1!=NULL && l2!=NULL){ if(l1->val > l2->val){ iter->next = l2; l2 = l2->next; }else{ iter->next = l1; l1 = l1->next; } iter = iter->next; } if(l1!=NULL){ iter->next = l1; } if(l2!=NULL){ iter->next = l2; } iter = dummy->next; delete dummy; return iter; } };

[Hard] No.23. Merge k Sorted Lists

Approach 1: Merge lists one by one

Time Complexity: O(kN) where k is the number of linked lists. We can merge two sorted linked list in O(N) time where N is the total number of nodes in two lists.

Space Complexity: O(1). We can merge two sorted linked list in O(1)O(1) space.

class Solution { public: ListNode* mergeKLists(vector<ListNode*>& lists) { ListNode* newL = NULL; for(int i = 0 ; i < lists.size() ; i++) { newL = mergerTwoLists(newL, lists[i]); } return newL; } ListNode* mergerTwoLists(ListNode* l1, ListNode* l2) { ListNode* dummy = new ListNode(); ListNode* iter = dummy; while(l1 != NULL && l2 != NULL) { if(l1->val > l2->val) { iter->next = l2; l2 = l2->next; }else { iter->next = l1; l1 = l1->next; } iter = iter->next; } if(l1 != NULL) { iter->next = l1; iter = iter->next; } if(l2 != NULL) { iter->next = l2; iter = iter->next; } return dummy->next; } };

Approach 2: Optimize Approach 1 by Priority Queue

Time Complexity: O(Nlogk) where k is the number of linked lists. N is the number of nodes in the final linked list.

Space Complexity: O(n) Creating a new linked list costs O(n) space. O(k)The code above present applies in-place method which cost O(1) space. And the priority queue (often implemented with heaps) costs O(k)O(k) space (it's far less than NN in most situations).

class Solution { private: struct cmp { bool operator() ( ListNode* l1, ListNode* l2){ return l1->val > l2->val; } }; public: ListNode* mergeKLists(vector<ListNode*>& lists) { int n = lists.size(); if(n == 0) return NULL; ListNode* dummy = new ListNode(0); ListNode* iter = dummy; priority_queue<ListNode, vector<ListNode*>, cmp > q; for(auto list : lists){ if(list != NULL) q.push(list); } while( q.empty() == false){ iter->next = q.top(); q.pop(); iter = iter->next; if(iter->next) q.push(iter->next); } return dummy->next; } };

Floyd's Tortoise and Hare (Cycle Detection)

[Medium] No.142 Linked List Cycle II

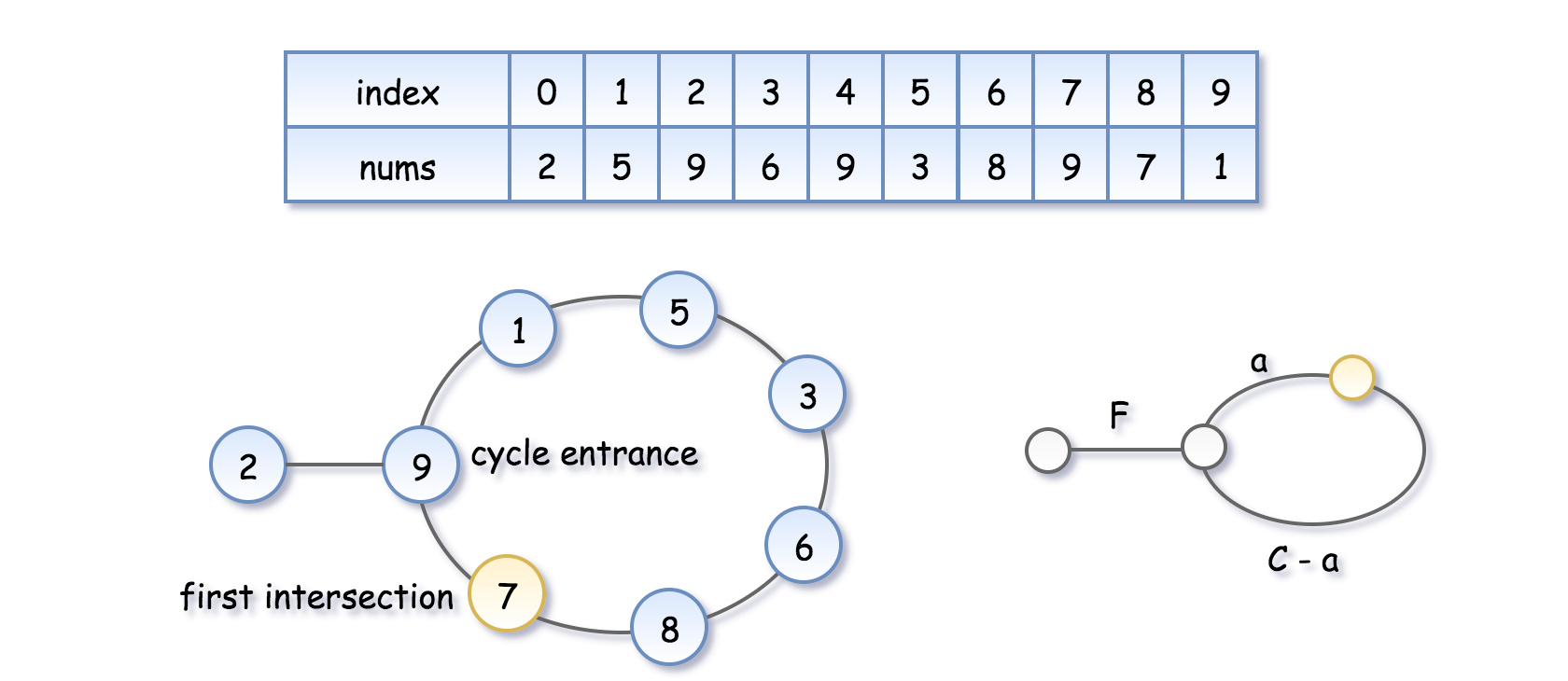
(The above image is from leetcode.com.)

step1. find the intersection points

step2. find the beginning of the cycle

use in linked list questions class Solution { public: ListNode *detectCycle(ListNode *head) { if(head == NULL || head->next == NULL) return NULL; ListNode* turtle = head; ListNode* hare = head; while(hare != NULL && hare->next != NULL) { turtle = turtle->next; hare = hare->next->next; if(turtle == hare) break; } turtle = head; while(turtle != hare && hare != NULL) { turtle = turtle->next; hare = hare->next; } return hare; } };

use in vector, string questions class Solution { public: int findDuplicate(vector<int>& nums) { int turtle = nums[0]; int hare = nums[0]; do{ turtle = nums[turtle]; hare = nums[nums[hare]]; }while(turtle != hare); turtle = nums[0]; while(turtle != hare) { turtle = nums[turtle]; hare = nums[hare]; } return hare; } };