Graph

Concept

How to avoid CYCLE while we are traversing the graph? Create a container to store visited elements.

An undirected graph is acyclic iff a DFS yields no back edges.

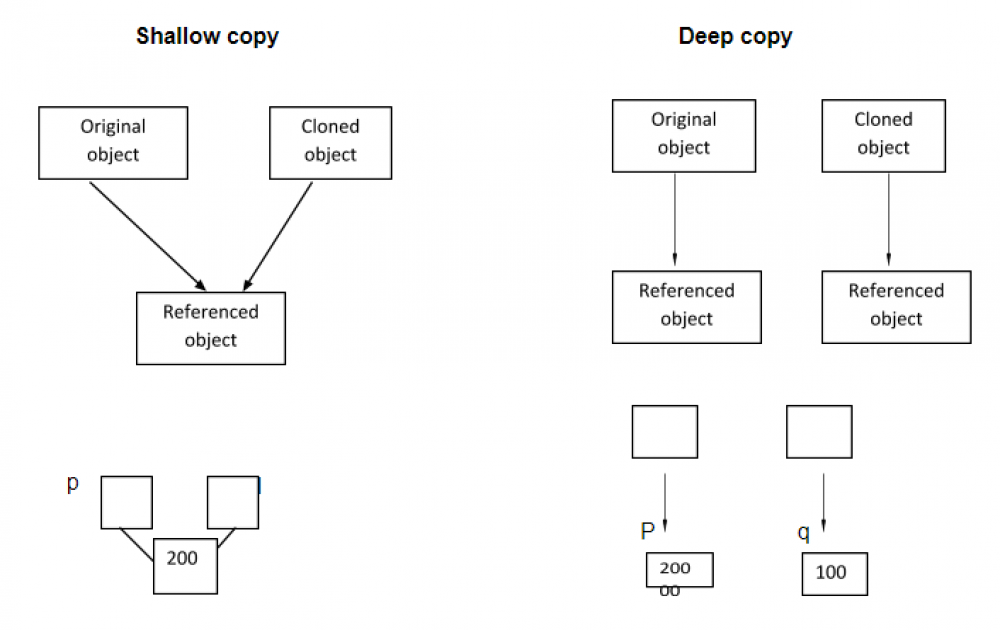
Deep Copy

A new oject is created without referencing the old one.

The copying process executes recursively.

Using "new" to deep copy every element.

(The above image is from http://en.wikipedia.org.)

Represent a graph

Adjacent List

save more space than adj matrix

Adjacent Matrix

[Medium] No.133 Clone Graph

Approach1: DFS

Time Complexity: O(N), where N is the number of nodes in the given graph.

Space Complexity: O(N), where N is the size of visited map. The stack would need O(H), where H is the maximum height of the graph. However, H <= N, overall, space complexity is O(N).

//DFS class Solution { public: unordered_map<Node*, Node*> visited; Node* cloneGraph(Node* node) { //base case if(node == NULL) return NULL; //traverse neighbors vector<Node*> iter = node->neighbors; Node* cur = new Node(node->val); visited[node] = cur; for(int i = 0 ; i < iter.size() ; i++) { //not visited if(visited.find(iter[i]) == visited.end()) { Node* nei = cloneGraph(iter[i]); cur->neighbors.push_back(nei); }else { cur->neighbors.push_back(visited[iter[i]]); } } return cur; } };

Approach2: BFS + queue

Time Complexity: O(N), where N is the number of nodes in the given graph.

Space Complexity: O(N), where N is the size of visited map. The queue would need O(W), where W is the maximum width of the graph. However, W <= N, overall, space complexity is O(N).

/* // Definition for a Node. class Node { public: int val; vector<Node*> neighbors; Node() { val = 0; neighbors = vector<Node*>(); } Node(int _val) { val = _val; neighbors = vector<Node*>(); } Node(int _val, vector<Node*> _neighbors) { val = _val; neighbors = _neighbors; } }; */ class Solution { public: Node* cloneGraph(Node* node) { if(node == NULL) return NULL; //original node, clone node unordered_map<Node*, Node*> visited; Node* dummy = new Node(node->val); queue<Node*> q; q.push(node); visited[node] = dummy; while(!q.empty()) { Node* cur = q.front(); q.pop(); //iterate through neighbors for(int i = 0 ; i < cur->neighbors.size() ; i++) { //not found if(visited.find(cur->neighbors[i]) == visited.end()) { Node* newNode = new Node(cur->neighbors[i]->val); visited[cur->neighbors[i]] = newNode; q.push(cur->neighbors[i]); } visited[cur]->neighbors.push_back(visited[cur->neighbors[i]]); } } return visited[node]; } };

Template - BFS in exploring graph

time complexity: O(V+E)

space complexity: O(E)

(The above image is from ASU SER501.)

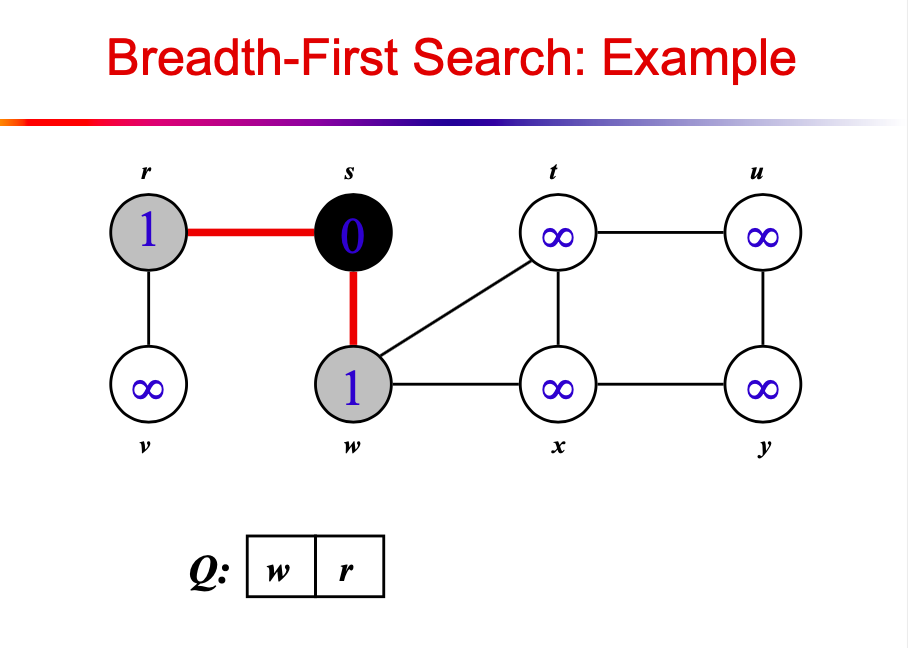
(The above image is from ASU SER501.)

Template - DFS in exploring graph

time complexity: O(V+E)

space complexity: O(V+E)

(The above image is from ASU SER501.)

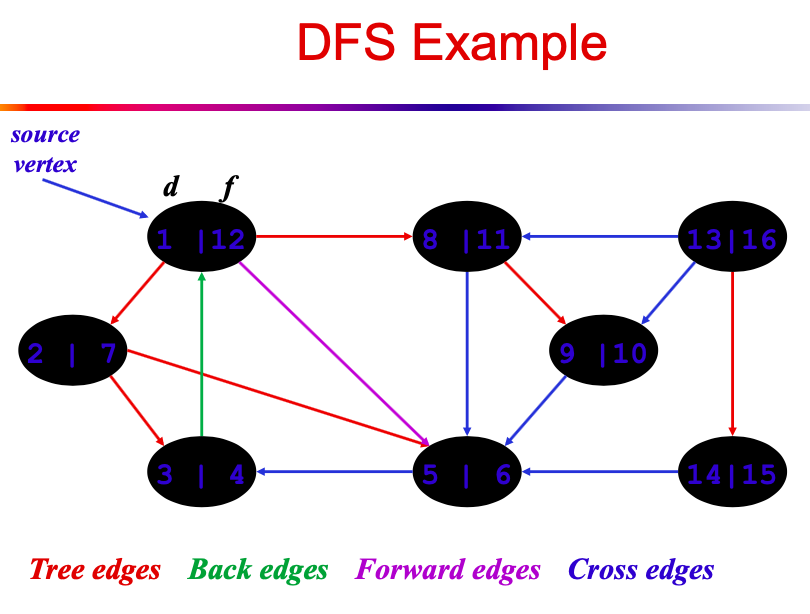
(The above image is from ASU SER501.)

(The above image is from ASU SER501.)

[Hard] No.1192 Critical Connections in a Network

Approach: DFS

Time Complexity: O(V+E), where V is the number of vertex in the given graph, E is the numbers of the given graph.

Space Complexity: O(V+E)

class Solution { public: int time = 0; vector<bool> visited; vector<int> startTime; vector<int> low;//lowest reachable node(time) vector<int> parent; vector<vector<int>> res; vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) { /*Initialise variables*/ vector<vector<int>> graph(n); visited.resize(n,false); startTime.resize(n,-1); low.resize(n,-1); parent.resize(n,-1); //build graph 因為是undirect graph, 所以起點和終點都要算 for(auto con : connections){ graph[con[0]].push_back(con[1]); graph[con[1]].push_back(con[0]); } //traverse each node for(int i = 0 ; i < n ; i++){ if(!visited[i]) dfs(graph, i); } return res; } void dfs(vector<vector<int>>& graph, int node){ visited[node] = true; startTime[node] = time; low[node] = time; //lowest reachable node(time) time++; int u = node; //neighbors for(auto v : graph[node]){ //not visited if(!visited[v]){ parent[v] = u; dfs(graph, v); //Update lowest node reachable from u low[u] = min(low[v], low[u]); //If no lower(than u) node is reachable from v , we have found bridge edge if(startTime[u] < low[v]){ res.push_back({u,v}); } } //visited, backtracking else{ if(parent[u] != v){ low[u] = min(low[v], low[u]); if(startTime[u] < low[v]){ res.push_back({u,v}); } } } } } };

Topological Sorting

Key concept: execute the node which doesn't have an incoming edge.

Time complexity: O(V+E), V is total vertices, E is total edges.

Tsort is for DAG(directed Acyclic Graph). Example in real life is dressing clothes.

May not have a unique answer.

(The above image is from wikipedia.org.)

Famous algorithm to implement tsort. Kahn's algo, DFS, Parallel algo.

Approach1 : BFS + indegree map + outdegree map

Approach2 : DFS + outdegree map

[Hard] No.269 Alien Dictionary