Tree

Binary Search Tree

Fact1. Inorder traversal of BST

class Solution { public: vector<int> vec; void inorderTraversal(ListNode* root) { if(root == NULL) return NULL; //finish left children first inorderTraversal(root->left); //add self into the vector vec.push_back(root->val); //finish the right children inorderTraversal(root->right); } };

Fact2. Successor (after node)

class Solution { public: ListNode* inorderTraversal(ListNode* root) { root = root->right; while(root->left != NULL) root = root->left; return root; } };

Fact3. Predecessor (before node)

class Solution { public: ListNode* inorderTraversal(ListNode* root) { root = root->left; while(root->right != NULL) root = root->right; return root; } };

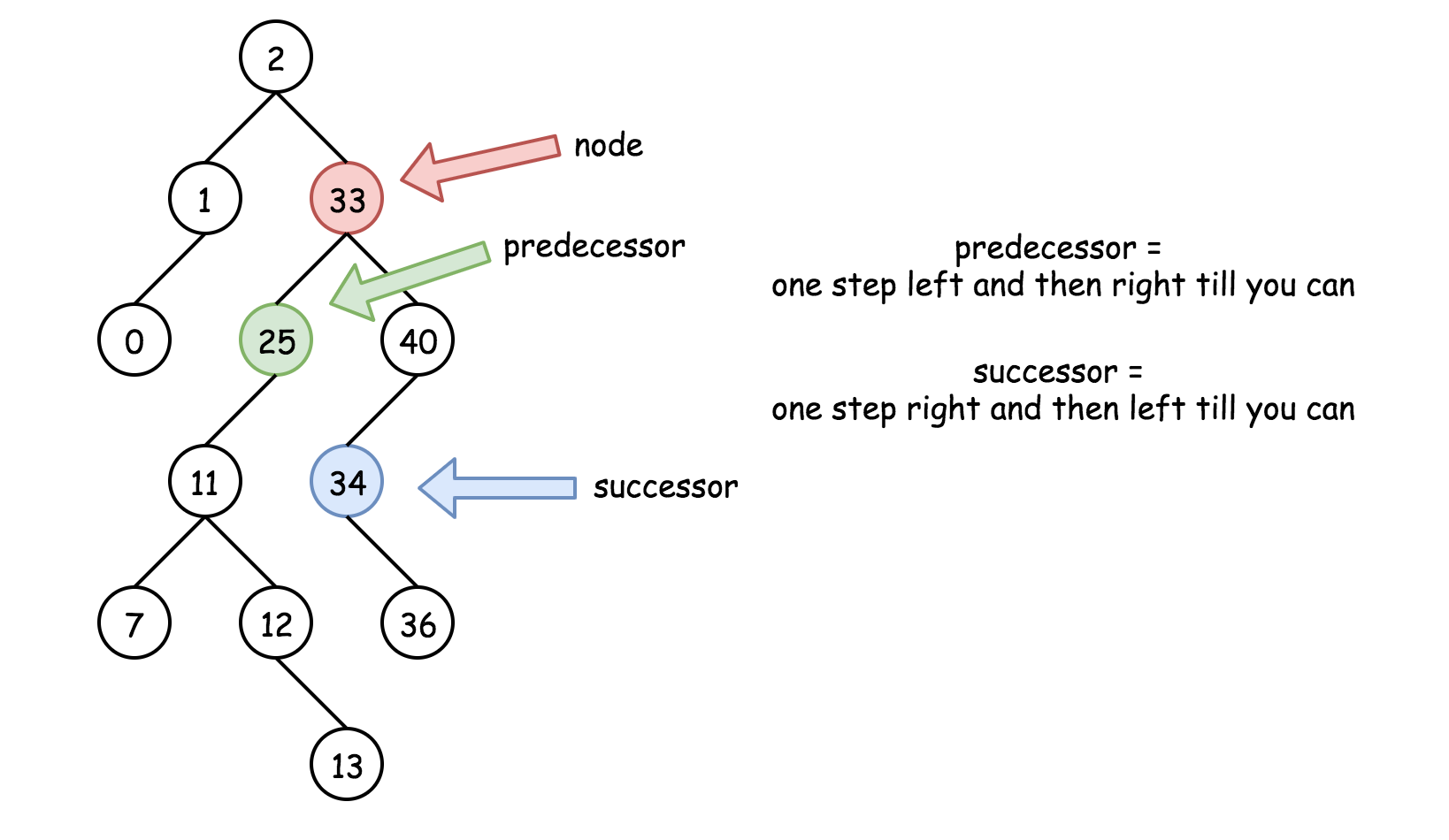
(The above image is from leetcode.com.)

[Medium] No.701 Insert into a Binary Search Tree

Approach: recursion

Time Complexity: O(H), H = logN if it's a balanced tree. O(H)/O(logN) in the average case, and O(N) in the worst case.

Space Complexity: O(H) to keep the recursion stack, where H is a tree height. H =logN for the balanced tree. O(N) in the worst case.

class Solution { public: TreeNode* insertIntoBST(TreeNode* root, int val) { if (root == NULL) { return new TreeNode(val); // return a new node if root is null } if (root->val < val) { // insert to the right subtree if val > root->val root->right = insertIntoBST(root->right, val); } else { // insert to the left subtree if val <= root->val root->left = insertIntoBST(root->left, val); } return root; } };

[Medium] No.450 Delete Node in a BST

Approach: recursion and finding successor

Time Complexity: O(H), H = logN if it's a balanced tree. O(H)/O(logN) in the average case, and O(N) in the worst case.

Space Complexity: O(H) to keep the recursion stack, where H is a tree height. H =logN for the balanced tree.

class Solution { public: TreeNode* deleteNode(TreeNode* root, int key) { if(root == NULL) return root; if(root->val == key){ //1. no children if(root->left == NULL && root->right == NULL){ return NULL; } //2. one child, swap root and the child if(root->left == NULL) return root->right; if(root->right == NULL) return root->left; //3. two child, find the inorder-successor TreeNode* iter = root; if(iter->right != NULL){ iter = iter->right; while(iter->left != NULL) iter = iter->left; } //iter will be the successor at this moment root->val = iter->val; root->right = deleteNode(root->right, iter->val); return root; }else if(root->val > key){ root->left = deleteNode(root->left, key); }else{ root->right = deleteNode(root->right, key); } return root; } };

[Medium] No.96. Unique Binary Search Trees

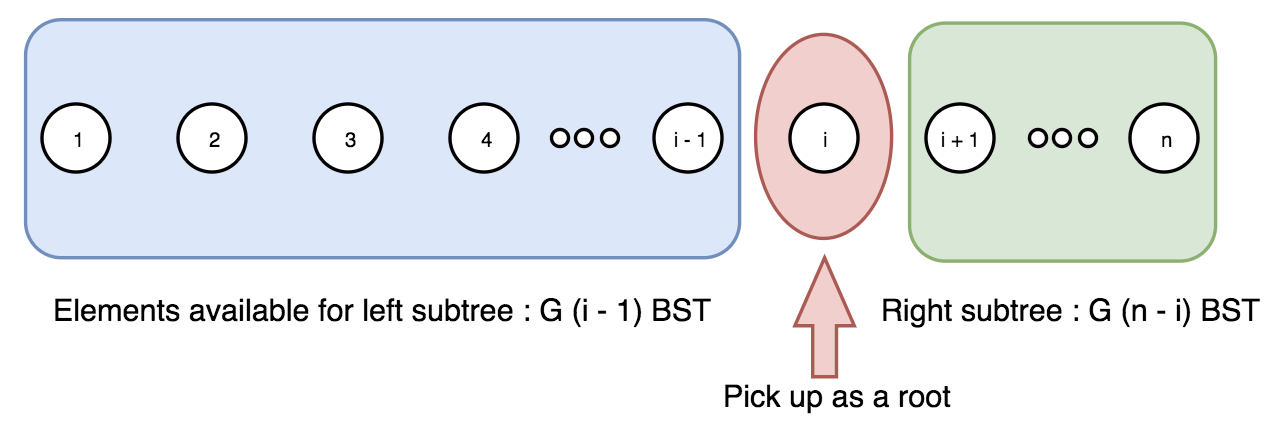
(The above image is from leetcode.com.)

Approach: dynamic programming

Time Complexity: O(N^2)

Space Complexity: O(N)

class Solution { public: int numTrees(int n) { vector<int> g(n+1,0); g[0] = 1; g[1] = 1; for(int i = 2 ; i <= n ; i++) { for(int j = 1 ; j <= i ; j++) { //length of two subtree g[i] += g[j-1] * g[i-j]; //g[2] = g[0] * g[1] } } return g[n]; } };