Greedy Algorithm

Concept

Making the locally optimal choice at each stage, but may not be the optimal choice for the global solution.

If a greedy algorithm can be proven to yield the global optimum for a given problem class, it typically becomes the method of choice because it is faster than other optimization methods like dynamic programming. Examples of such greedy algorithms are Kruskal's algorithm and Prim's algorithm for finding minimum spanning trees, and the algorithm for finding optimum Huffman trees.

In greedy alogorithm questions, it usually does not encounter SAME previous subproblems, which are what DP questions have.

Minimum spanning trees (MST)

1.Finding minimum spanning FOREST in a DISCONNECTED graph : includes every vertex, where the sum of the weights of all the edges in the tree is minimized.

2.Finding minimum spanning TREE in a CONNECTED graph : composed of a minimum spanning tree for each connected component.

Kruskal's algorithm (add edges)

Approach: disjoint-set (Union-find)

Prim's algorithm (add vertex)

Different from Dijkstra's algo : no need to acuumulate values for each node, only need to find local optimal edge.

Approach: BFS

Time complexity:

1.Binary heap(priority queue)=> O(ElogV), where E is the number of total edges and V is the number of vertex.

2.Fibonacci heap => O(VlogV + E).

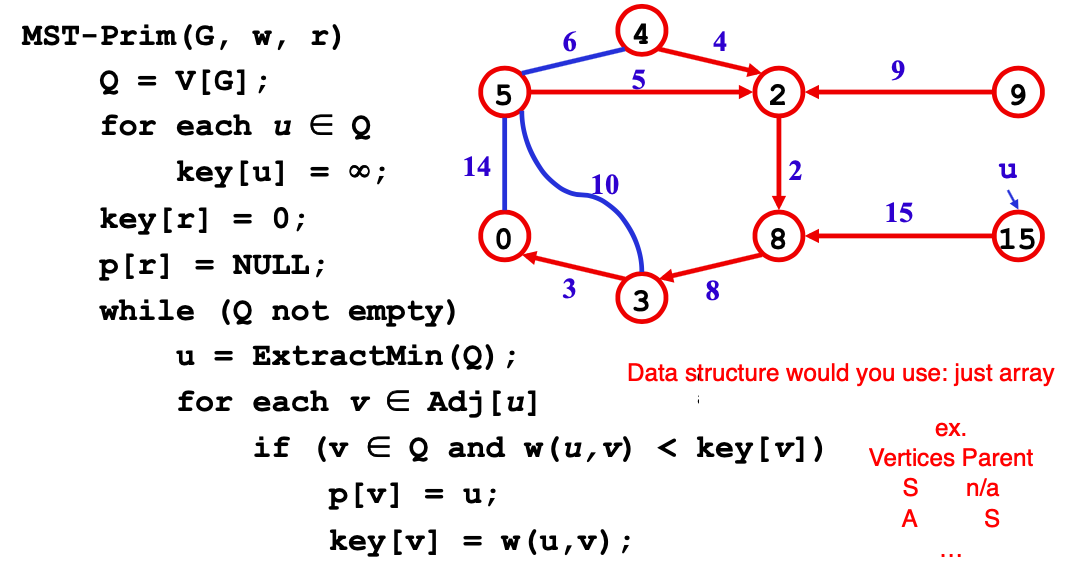
(The above image is from ASU SER501.)

Graph search and finding a shortest path

Dijkstra's algorithm

1.Using BFS to traverse each vertex.

2.Should be a connected, all positive weights graph. Algorithm applies to both directed and undirected graph.

3.If there exists a negative weight of edges, it will cause cycle and can't find a shortest path.

4.A key technique in shortest path algorithms is relaxation.

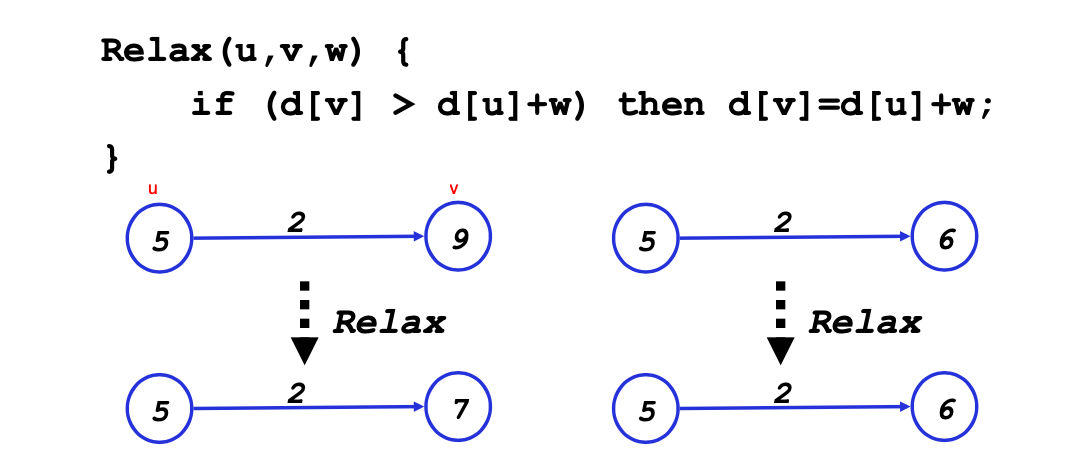
(The above image is from ASU SER501.)

5.May not result in a MST.

Approach: BFS

Time complexity:

1.Binary heap(priority queue) => O(ElogV), where E is the total number of edges and V is the total number of vertex. Look here for explaination

2.Fibonacci heap => O(VlogV + E).

Space complexity: O(V)

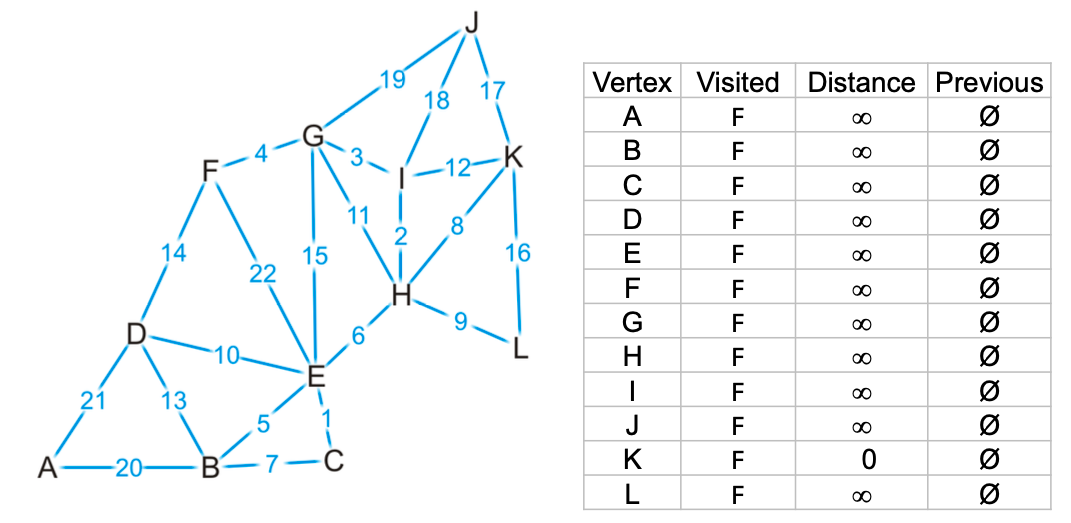
(The above image is from ASU SER501.)

Decision tree

Not garantee to find an optimal solution

Huffman tree

Travelling salesman problem

[Medium] No.763 Partition Labels

Approach: Greedy

Time Complexity: O(N), where N is the length of input string.

Space Complexity: O(1), keep data structure last of not more than 26 characters.

class Solution { public: vector<int> partitionLabels(string S) { vector<int> last(26,0); //document the last index of each letter for(int i = 0 ; i < S.size() ; i++) { last[S[i] - 'a'] = i; } int start = 0, end = 0; vector<int> ans; for(int i = 0 ; i < S.size() ; i++) { end = max(end, last[S[i] - 'a']); if(end == i) { ans.push_back(end - start + 1); start = end + 1; } } return ans; } };

[Medium] No.678 Valid Parenthesis String

Approach: Greedy

Time Complexity: O(N), where N is the length of input string.

Space Complexity: O(1)

class Solution { public: bool checkValidString(string s) { int maxDiff = 0, minDiff = 0; for (char c : s) { maxDiff += (c == '(' || c == '*') ? 1 : -1; minDiff += (c == ')' || c == '*') ? -1 : 1; if (maxDiff < 0) return false; minDiff = max(0, minDiff); } return minDiff == 0; } };