Tree

Heap

Heap is a tree-based data structure.

Binary Heap

A binary heap is a complete binary tree. There are max-heap and min-heap. Binary heaps are a common way of implementing priority queues. Thus, we can say priority queue uses a heap as data structure.

Operations on heap

make_heap(iter_first, iter_last)

Making a vector into a MAX heap.

make_heap(iter_first, iter_last, comp)

Making a vector into a MIN heap. The comp parameter is greater().

* time complexity: O(NlogN), since heapify costs O(logN) and build-heap makes O(N) calls. However, O(NlogN) is the upperbound,though correct. The tighter bound can be O(N). You represent the heap as an array and heap is based on a complete binary tree. The two elements below the i'th element are at positions 2*i+1 and 2*i+2. If the array has n elements then, starting from the end, take each element, and let it "fall" to the right place in the heap. This is O(n) to run.

* space complexity: Because the make_heap will rearrange the elements in the vector, basically the space for heap is the same as the vector, which is O(N) for heap itself. There might only few variables that are used for doing swaps.

using namespace std; int main() { vector<int> vec = { 4, 9, 7, 8, 11}; // using make_heap() to making a vector into a max heap make_heap(vec.begin(), vec.end()); // front() function cout << "The maximum number in the heap is:"; cout << vec.front(); }

using namespace std; int main() { vector<int> vec = { 4, 9, 7, 8, 11}; // using make_heap() to making a vector into a max heap make_heap(vec.begin(), vec.end(), greater<int>()); // front() function cout << "The minimum number in the heap is:"; cout << vec.front(); }

front()

Retrieve the root value in this heap, either a maximum or a minimum value depending on which heap you built.

push_heap(iter_first, iter_last)

Insert a new value into MAX heap.

push_heap(iter_first, iter_last, comp)

Insert a new value into MIN heap. The comp parameter is greater().

//MAX HEAP vec.push_back(99); push_heap (vec.begin(), vec.end()); cout << "max heap after push: " << v.front(); //MIN HEAP vec.push_back(99); push_heap (vec.begin(), vec.end(), greater<int>()); cout << "min heap after push: " << v.front();

pop_heap(iter_first, iter_last)

Delete the maximum or minimum value in the heap, and it depends on which heap you use.

When we use pop_heap, it will move the maximum or minimum value to the back of the vector, and heapify the elements from 0 to last-2. You need to pop_back the element in the vector to finish the operation.

pop_heap (vec.begin(), vec.end()); vec.pop_back();

Max Heap

Each node is BIGGER than it's left and right children.

Min Heap

Each node is SMALLER than it's left and right children.

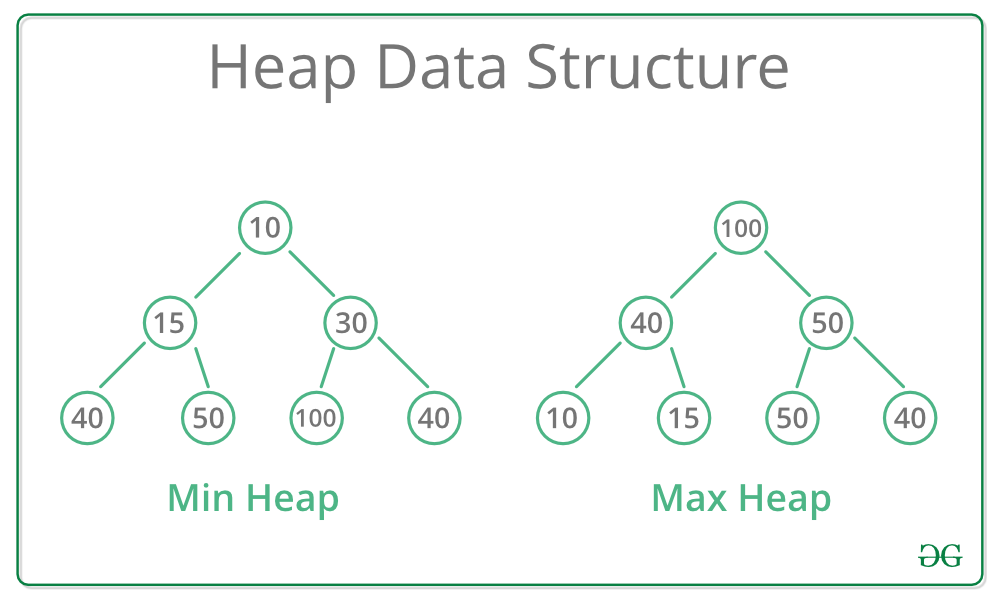
(The above image is from https://www.geeksforgeeks.org/heap-data-structure/.)

Priority Queue

Even though priority queue acts like a queue, it implements binary heap data strcuture.

Operations on priority queue

empty()

Return bool value. True if the priority queue is empty, otherwise return false.

size()

Return number of elements in the priority queue.

top()

Triger front() once.

pop()

Triger push_back() once and then push_heap() once. Same way and order as heap does.

push()

Triger pop_heap() once and then pop_back() once. Same way and order as heap does.

// priority_queue::empty #include <iostream> // cout #include <queue> // priority_queue int main () { priority_queue<int> mypq; int sum (0); for (int i=1;i<=10;i++) mypq.push(i); while (!mypq.empty()) { sum += mypq.top(); mypq.pop(); } cout << "total: " << sum << '\n'; return 0; }

priority_queue(int)

Decreasing order

priority_queue, greater>

Increasing order

[Medium] No.973 K Closest Points to Origin

Approach: priority queue

Time Complexity: O(NlogN), where N is the number of nodes in the vector, and heap sorting costs O(NlogN).

Space Complexity: O(N), where N is the number of nodes need to store in the priority queue.

class Solution { public: typedef pair<int,pair<int,int>> PAIR; vector<vector<int>> kClosest(vector<vector<int>>& points, int K) { priority_queue<PAIR, vector<PAIR>,greater<PAIR>> pq; vector<vector<int>> ans; for(auto point : points) { pq.push({point[0]*point[0] + point[1]*point[1], {point[0],point[1]}}); } while(!pq.empty() && K > 0) { pair<int,pair<int,int>> cur = pq.top(); pq.pop(); ans.push_back({cur.second.first, cur.second.second}); K--; } return ans; } };